5. 补充:原码反码补码和进制¶
5.1. 进制¶
进制也就是进位制,是人们规定的一种进位方法。 对于任何一种进制—X进制,就表示某一位置上的数运算时是逢X进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。
十进制 |
二进制 |
八进制 |
十六进制 |
|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
10 |
2 |
2 |
3 |
11 |
3 |
3 |
4 |
100 |
4 |
4 |
5 |
101 |
5 |
5 |
6 |
110 |
6 |
6 |
7 |
111 |
7 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
A |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
5.1.1. Go语言如何表示相应进制数¶
十进制 |
以正常数字1-9开头,如123 |
|---|---|
八进制 |
以 |
十六进制 |
以 |
二进制 |
以 |
5.1.2. 二进制¶
二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。
注解
当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。
术语 |
含义 |
|---|---|
bit(比特) |
一个二进制代表一位,一个位只能表示0或1两种状态。数据传输是习惯以“位”(bit)为单位。 |
Byte(字节) |
一个字节为8个二进制,称为8位,计算机中存储的最小单位是字节。数据存储是习惯以“字节”(Byte)为单位。 |
WORD(双字节) |
2个字节,16位 |
DWORD |
两个WORD,4个字节,32位 |
1b |
1bit,1位 |
1B |
1Byte,1字节,8位 |
1k,1K |
1024 |
1M(1兆) |
1024k, 1024*1024 |
1G |
1024M |
1T |
1024G |
1Kb(千位) |
1024bit,1024位 |
1KB(千字节) |
1024Byte,1024字节 |
1Mb(兆位) |
1024Kb = 1024 * 1024bit |
1MB(兆字节) |
1024KB = 1024 * 1024Byte |
十进制转化二进制的方法:用十进制数除以2,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果。

package main
import (
"fmt"
)
func main() {
fmt.Printf("%#b", 56)
}
0b111000
警告
计算机中所有数据都是以2进制方式存储的,在Go语言中,我们是可以直接书写二进制的!
package main
import (
"fmt"
)
func main() {
var a int8 = 0b111000
fmt.Println(a)
}
56
5.1.3. 八进制¶
八进制,Octal,缩写OCT或O,一种以8为基数的计数法,采用0,1,2,3,4,5,6,7八个数字,逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。
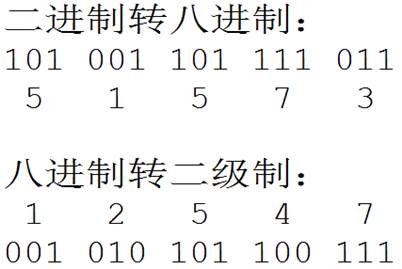
八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),因此常应用在计算机语言中。
package main
import (
"fmt"
)
func main() {
var a int32 = 0b101001101111011
var b int32 = 0o12547
fmt.Printf("%#O\n", a)
fmt.Printf("%#b\n", b)
}
0o051573
0b1010101100111
十进制转化八进制的方法:
用十进制数除以8,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果。

package main
import (
"fmt"
)
func main() {
var a = 567
fmt.Printf("%#O\n", a)
}
0o01067
5.1.4. 十六进制¶
十六进制(英文名称:Hexadecimal),同我们日常生活中的表示法不一样,它由0-9,A-F组成,字母不区分大小写。与10进制的对应关系是:0-9对应0-9,A-F对应10-15。
十六进制的数和二进制数可以按位对应(十六进制一位对应二进制四位),因此常应用在计算机语言中。

package main
import (
"fmt"
)
func main() {
var a = 0b010101111010101101010111110101110000
var b = 0xAB42D
fmt.Printf("%#X\n", a)
fmt.Printf("%#b\n", b)
}
0X57AB57D70
0b10101011010000101101
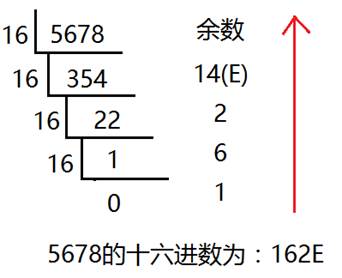
十进制转化十六进制的方法:
用十进制数除以16,分别取余数和商数,商数为0的时候,将余数倒着数就是转化后的结果。
package main
import (
"fmt"
)
func main() {
var a = 5678
fmt.Printf("%#X\n", a)
}
0X162E
5.2. 计算机内存数值存储方式¶
5.2.1. 原码¶
一个数的原码(原始的二进制码)有如下特点:
最高位做为符号位,
0表示正,为1表示负其它数值部分就是数值本身绝对值的二进制数
负数的原码是在其绝对值的基础上,最高位变为
1
下面数值以1字节的大小描述:
十进制数 |
原码 |
|---|---|
+15 |
0000 1111 |
-15 |
1000 1111 |
+0 |
0000 0000 |
-0 |
1000 0000 |
原码表示法简单易懂,与带符号数本身转换方便,只要符号还原即可,但当两个正数相减或不同符号数相加时,必须比较两个数哪个绝对值大,才能决定谁减谁,才能确定结果是正还是负,所以原码不便于加减运算。
5.2.2. 反码¶
对于正数,反码与原码相同
对于负数,符号位不变,其它部分取反(
1变0,0变1)
十进制数 |
反码 |
|---|---|
+15 |
0000 1111 |
-15 |
1111 0000 |
+0 |
0000 0000 |
-0 |
1111 1111 |
反码运算也不方便,通常用来作为求补码的中间过渡。
5.2.3. 补码¶
在计算机系统中,数值一律用补码来存储。
补码特点:
对于正数,原码、反码、补码相同
对于负数,其补码为它的反码加
1补码符号位不动,其他位求反,最后整个数加
1,得到原码
十进制数 |
补码 |
|---|---|
+15 |
0000 1111 |
-15 |
1111 0001 |
+0 |
0000 0000 |
-0 |
0000 0000 |
5.2.3.1. 补码的意义¶
5.2.3.1.1. 示例1:¶
用8位二进制数分别表示+0和-0
十进制数 |
原码 |
|---|---|
+0 |
0000 0000 |
-0 |
1000 0000 |
十进制数 |
反码 |
|---|---|
+0 |
0000 0000 |
-0 |
1111 1111 |
不管以原码方式存储,还是以反码方式存储,0也有两种表示形式。为什么同样一个0有两种不同的表示方法呢?
但是如果以补码方式存储,补码统一了零的编码:
十进制数 |
补码 |
|---|---|
+0 |
0000 0000 |
-0 |
10000 0000 由于只用8位描述,最高位1丢弃,变为 0000 0000 |
5.2.3.1.2. 示例2:¶
计算9-6的结果
以原码方式相加:
十进制数 |
原码 |
|---|---|
9 |
0000 1001 |
-6 |
1000 0110 |

结果为-15,不正确。
以补码方式相加:
十进制数 |
补码 |
|---|---|
9 |
0000 1001 |
-6 |
1111 1010 |

最高位的1溢出,剩余8位二进制表示的是3,正确。
在计算机系统中,数值一律用补码来存储,主要原因是:
统一了零的编码
将符号位和其它位统一处理
将减法运算转变为加法运算
两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃
5.2.4. 数值溢出¶
当超过一个数据类型能够存放最大的范围时,数值会溢出。
有符号位最高位溢出的区别:符号位溢出会导致数的正负发生改变,但最高位的溢出会导致最高位丢失。
数据类型 |
占用空间 |
取值范围 |
|---|---|---|
int8 |
1字节 |
-128到 127 |
uint8 |
1字节 |
0 到 255 |
package main
import "fmt"
func main() {
// 符号位溢出会导致数的正负发生改变
var num1 int8 = 127
num1 += 2
fmt.Printf("b: %b v: %v\n", num1, num1)
/*
原码 = 0111 1111
补码 = 0111 1111
+2
补码 = 1000 0001
原码 = 1111 1110 +1 = 1111 1111
= -127
*/
//最高位的溢出会导致最高位丢失
var num2 uint8 = 255
num2 += 1
fmt.Printf("b: %b v: %v\n", num2, num2)
/*
补码 = 1111 1111
+1
补码 = 1 0000 0000 //最高位溢出
补码 = 0000 0000
原码 = 0000 0000
原码 = 0
*/
}
b: -1111111 v: -127
b: 0 v: 0
5.3. 字节序¶
现代CPU计算时一次都能装载多个字节(如32位计算机一次装载4字节),多字节的数值在内存中高低位的排列方式会影响所表示的数值,以int32类型的数值169756310(十六进制表示为:0x0103070f;二进制表示为:0b 00000001 00000011 00000111 00001111)为例,在内存中用4个字节存储,4个字节的内容分别是0x01(00000001)、0x03(00000011)、0x07(00000111)、0x0f(00001111)。根据字节高低位排序方式的不同,可以分为:大端字节序(big endian)和 小端字节序(little endian)。
计算机处理字节序的时候,不知道什么是高位字节,什么是低位字节。它只知道按顺序读取字节,先读第一个字节,再读第二个字节。 如果是大端字节序,先读到的就是高位字节,后读到的就是低位字节。小端字节序正好相反。 理解这一点,才能理解计算机如何处理字节序

5.3.1. 大端字节序¶
大端字节序是指一个整数的高位字节(如上例中的0x01)存储在内存的低地址处,可以理解为数值的高位部分靠前存储。以前面的0x0103070f为例,假如存储在内存中的起始地址为0x12345678,则0x0103070f在内存中的存储为:
地址0x12345678处存储内容为:0x01(00000001)
地址0x12345679处存储内容为:0x03(00000011)
地址0x1234567a处存储内容为:0x07(00000111)
地址0x1234567b处存储内容为:0x0f(00001111)
小技巧
大端字节序:高位字节在前,低位字节在后,这是人类读写数值的方法。
5.3.2. 小端字节序¶
和大端字节序相反,小端字节序把数值的低位字节存储在内存的低地址处,即低位部分靠前存储,0x0103070f在内存中的存储为:
地址0x12345678处存储内容为:0x0f(00001111)
地址0x12345679处存储内容为:0x07(00000111)
地址0x1234567a处存储内容为:0x03(00000011)
地址0x1234567b处存储内容为:0x01(00000001)
小技巧
小端字节序:低位字节在前,高位字节在后
5.3.3. 主机字节序¶
现代计算机大多采用小端字节序,所以小端字节序又叫主机字节序。
5.3.4. 网络字节序¶
不同的计算机可能会采用不同的字节序,甚至同一计算机上不同进程会采用不同的字节序,如JAVA虚拟机采用大端字节序,可能和采用小端字节序计算机上的其他进程不同。所以在网络通信(或进程间通信)时,如果都按自己存储的顺序收发数据,有可能会出现一些『误解』。比如采用大端字节序的进程按自己字节序发数据0x0103070f给一个小端字节序进程,发送的内容为:00000001 00000011 00000111 00001111。采用小端字节序的进程接收到数据后,按照小端字节序的定义,00000001是低位字节内容,00001111是高位字节内容,这样就把0x0103070f理解成了0x0f070301。
为了避免这个问题,约定数据在不同计算机之间传递时都采用大端字节序,也叫作网络字节序。
通信时,发送方需要把数据转换成网络字节序(大端字节序)之后再发送,接收方再把网络字节序转成自己的字节序。上面大端发给小端的例子,大端发送时不需要做处理,直接按自己的字节序发送,小端方接收时把接收到的数据转换成小端字节序后再使用。
注解
只有读取的时候,才必须区分字节序,其他情况都不用考虑
5.3.5. 通识¶
Inter X86 CPU 使用小端模式
网络传输,基本都是大端模式
Windows、Linux使用小端模式
Mac OS 使用大端模式
Java虚拟机使用大端模式
注解
记不住没关系,单独记住网络传输是大端序